Towards Stable 3D Object Detection

Abstract

In autonomous driving, the temporal stability of 3D object detection greatly impacts the driving safety. However, the detection stability cannot be accessed by existing metrics such as mAP and MOTA, and consequently is less explored by the community. To bridge this gap, this work proposes Stability Index (SI), a new metric that can comprehensively evaluate the stability of 3D detectors in terms of confidence, box localization, extent, and heading. By benchmarking state-of-the-art object detectors on the Waymo Open Dataset, SI reveals interesting properties of object stability that have not been previously discovered by other metrics. To help models improve their stability, we further introduce a general and effective training strategy, called Prediction Consistency Learning (PCL). PCL essentially encourages the prediction consistency of the same objects under different timestamps and augmentations, leading to enhanced detection stability. Furthermore, we examine the effectiveness of PCL with the widely-used CenterPoint, and achieve a remarkable SI of 86.00 for vehicle class, surpassing the baseline by 5.48. We hope our work could serve as a reliable baseline and draw the community's attention to this crucial issue in 3D object detection.

🔥 The Importance of Stability Issues

Detection stability encompasses more than mere robustness; it extends to the broader context of ensuring human safety in autonomous driving. As exemplified in the above figures, unstable detections, on both confidence scores and bounding boxes, can result in abnormal velocity estimated by tracking. These erroneous estimations may trigger false judgement on the behaviors of surrounding agents, potentially misleading the ego-vehicle to make improper or even hazardous decisions.

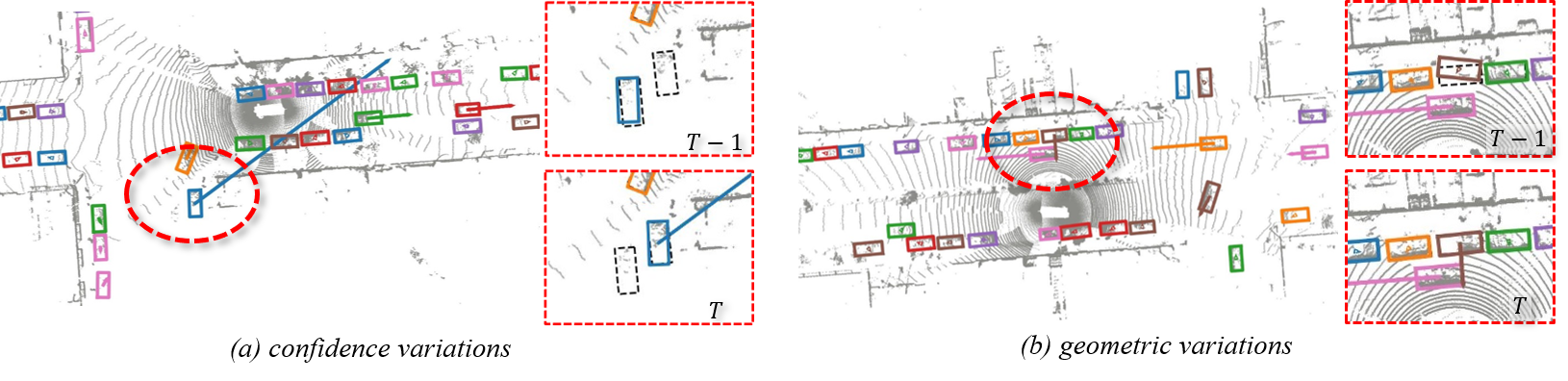
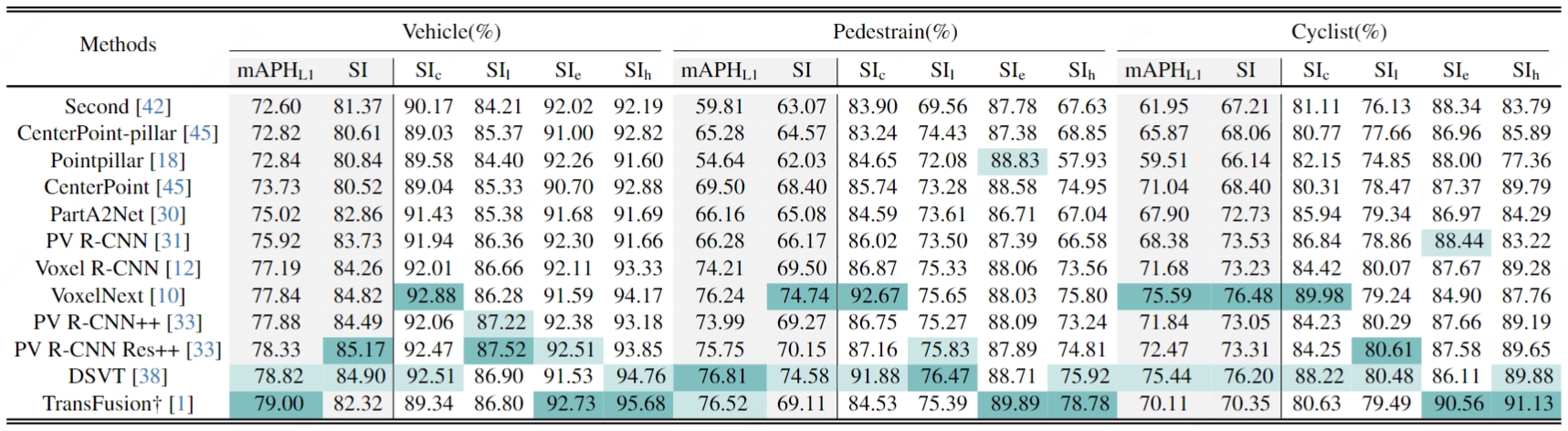
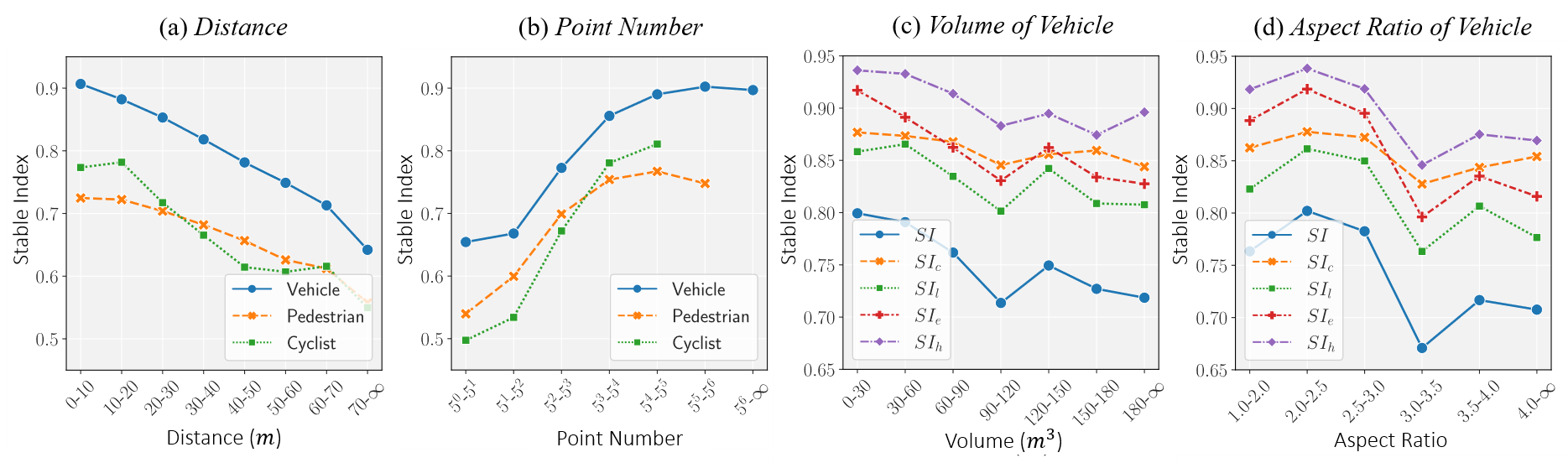
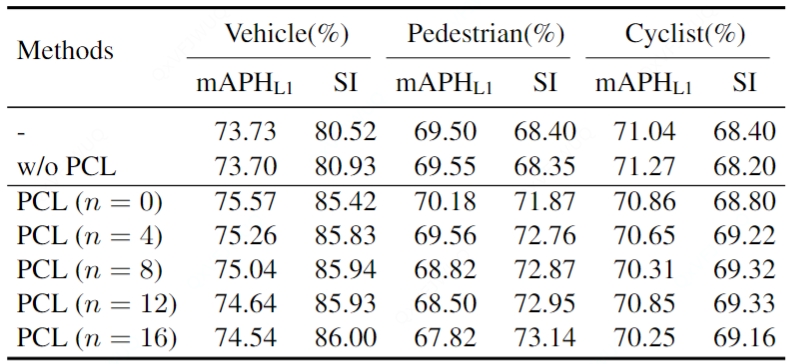
🚀 3D Detection Stability Evaluation and Improvment

Principles in Stability Metric Design

Through the detailed analysis of stability and exploration of potential solutions, we identify four key properties that an effective metric should meet:

Comprehensiveness: The metric should comprehensively reflect influences from all relevant detection elements.
Homogeneity: Influences caused by all elements should be well-processed into unified physical units.
Symmetry: The metric values should be consistent when applied to both forward and reverse inputs.
Marginal Unimodality: For each element with others fixed, the metric should be unimodal w.r.t. its stability.

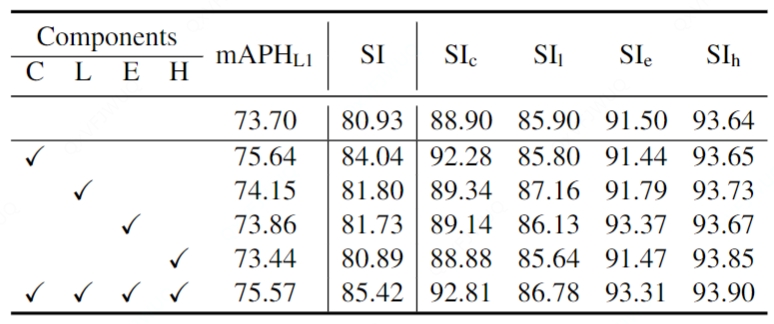
Stability Index

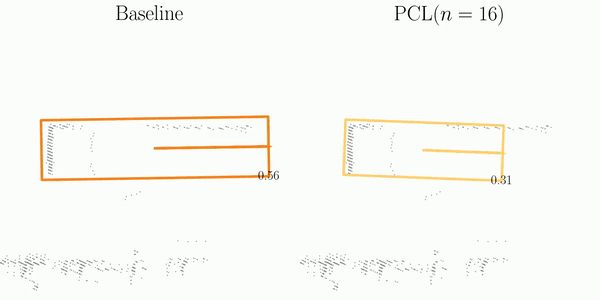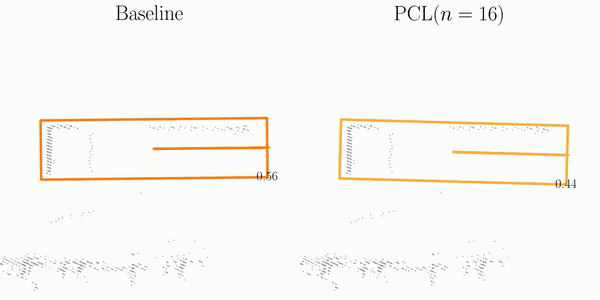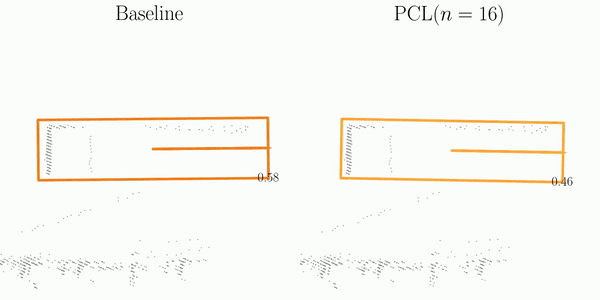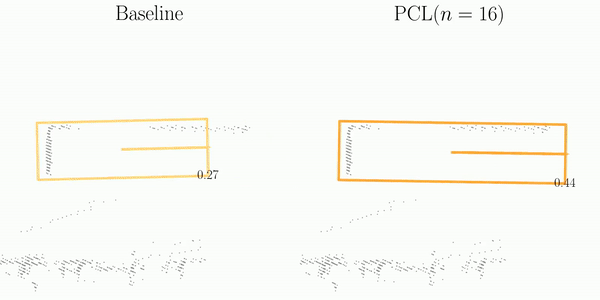
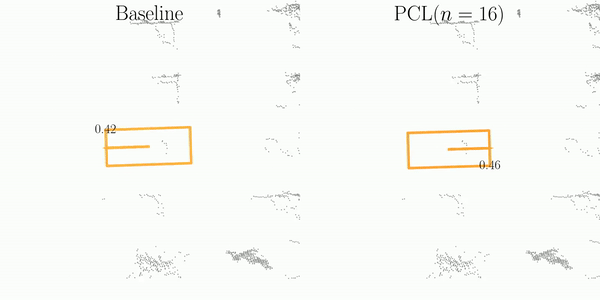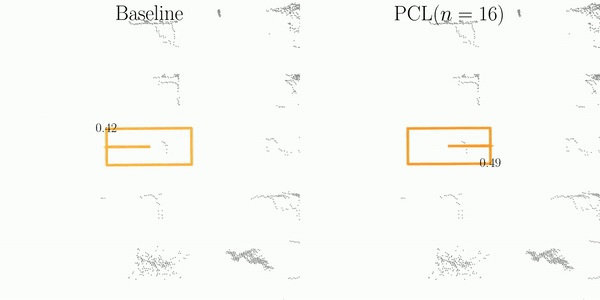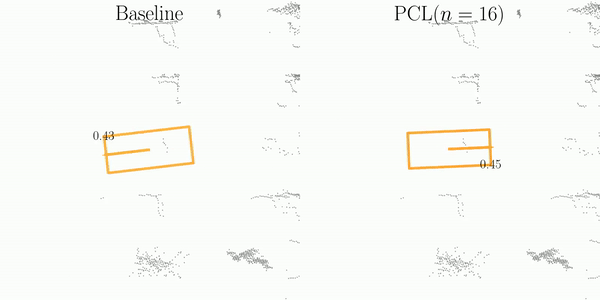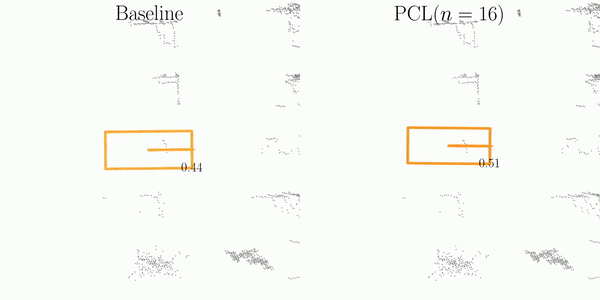
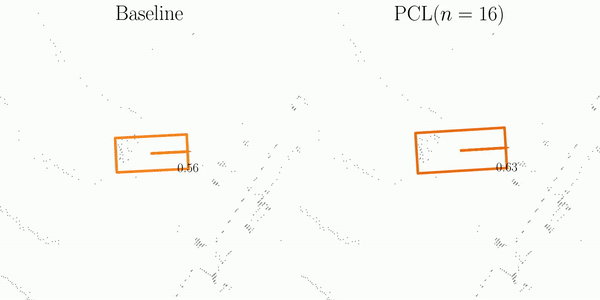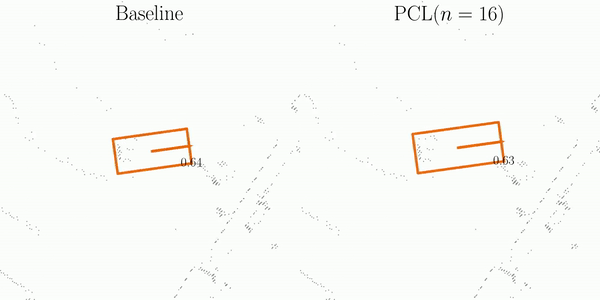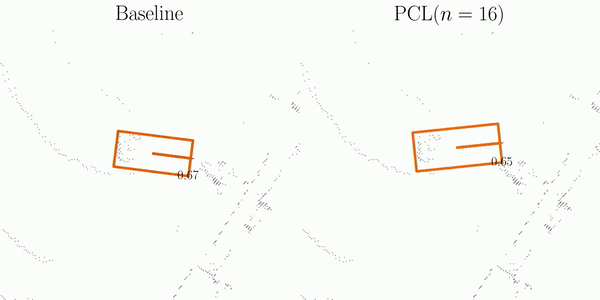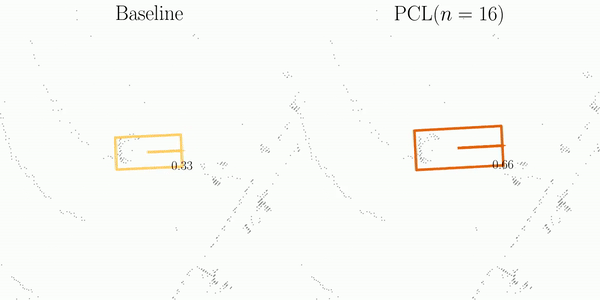
We assess the stability of object pairs in consecutive frames and denote the metric as Stability Index (SI). As illustrated in the figure, SI is comprised of three main steps: Matching, Projection, and Decoupling.

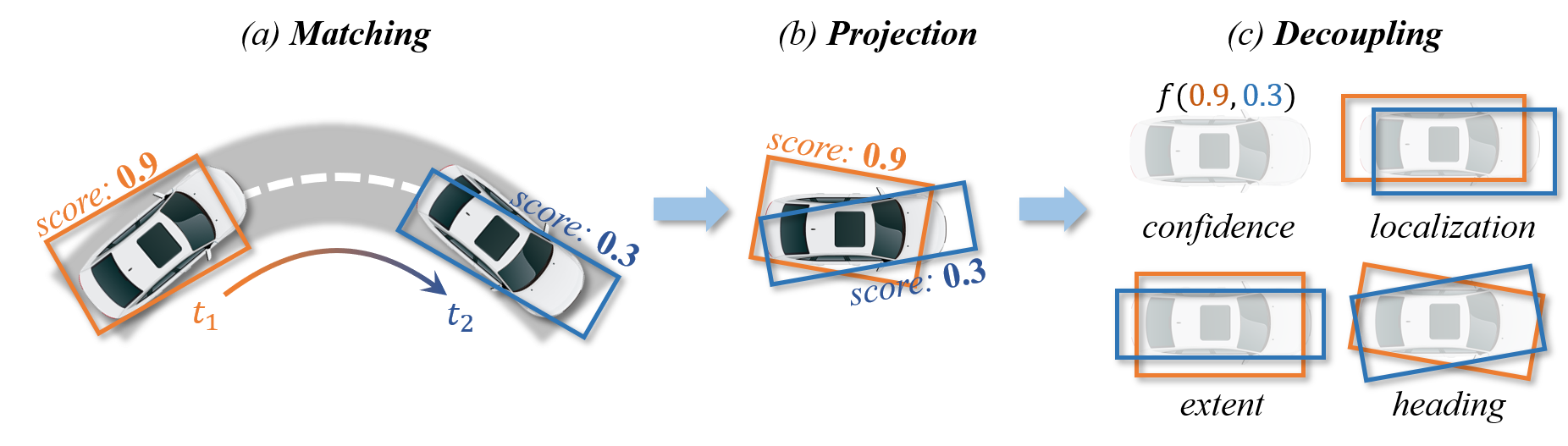
The orange and blue boxes represent the best matches between the predictions and the ground-truths searched by the Hungarian algorithm. These boxes are subsequently associated across frames using their object ID labels. After projecting predictions into a pre-built pivot box, SI decouples them into element-wise computations, which are then aggregated for the final assessment of detection stability. For the details of the procedure of computing SI, please refer to our paper.

Prediction Consistency Learning

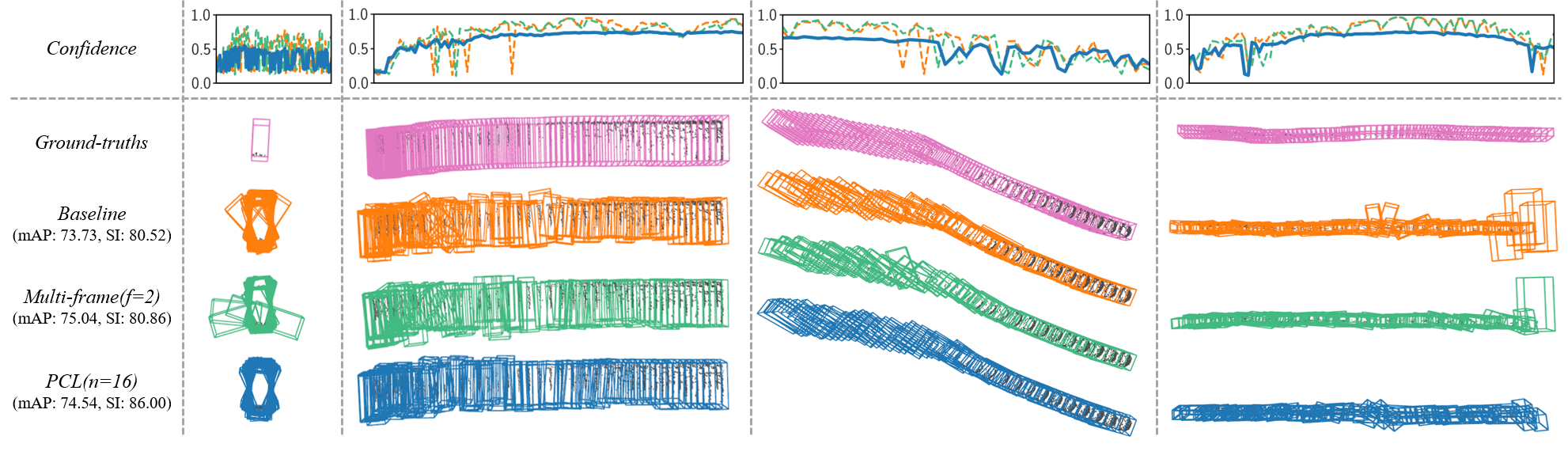
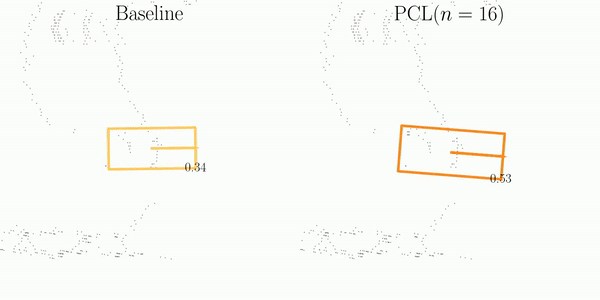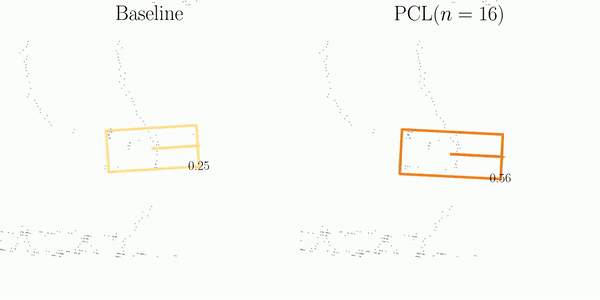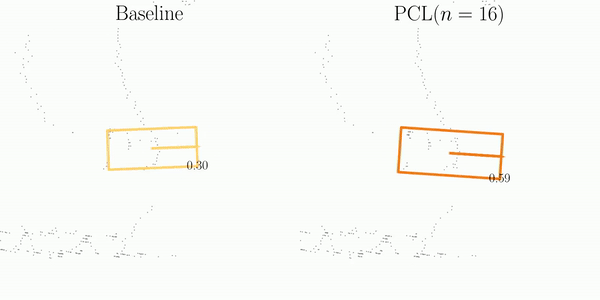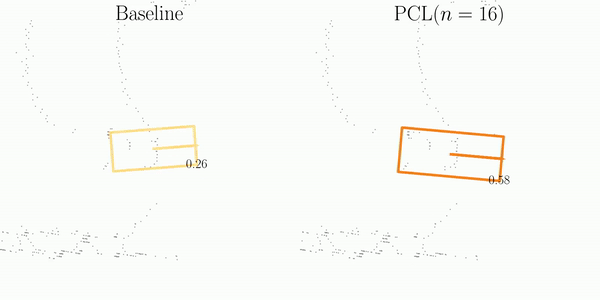
Beyond the design of the metric, we introduce a general and effective training strategy named Consistency Learning (PCL), to boost the detection stability of 3D object detectors.

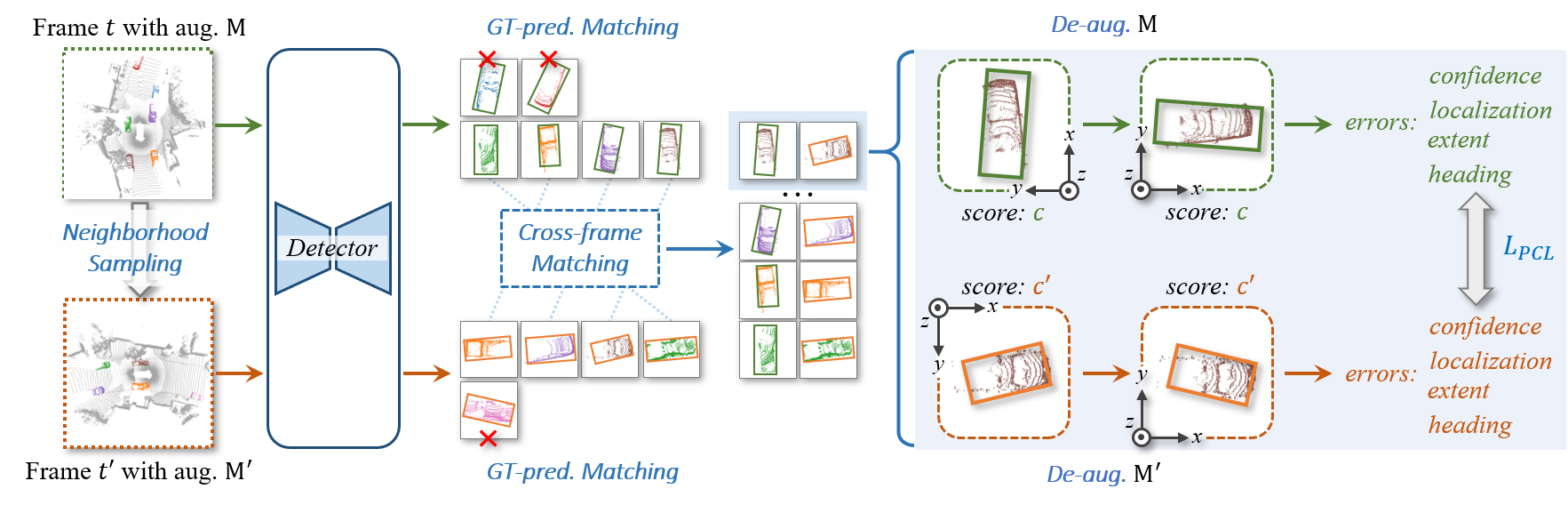
In each iteration, PCL samples a pair of frames at neighboring timestamps t and t', and applies augmentations M and M' to the paired samples. GT-prediction matching and cross-frame matching then collaboratively associate the detector's predictions from the same objects between the two frames. After the de-augmentation procedure, PCL calculates the prediction errors in terms of confidence, localization, extent, and heading, which are defined in the object self-coordinate system. Finally, PCL penalizes the error disparities among all prediction pairs to enforce the temporal consistency. In the figure, pred. and aug. represent prediction and augmentation, respectively. Please refer to the paper for details.

📺 Quantitative and Qualitative Results

Benchmark on the Waymo Open Dataset

Analysis on the Waymo Open Dataset

Results of PCL

Visualizations

Confidence	Localization

Extent	Heading

📖 Citation


@inproceedings{wang2024towards,
  title={Towards stable 3d object detection},
  author={Wang, Jiabao and Meng, Qiang and Liu, Guochao and Yan, Liujiang and Wang, Ke and Cheng, Ming-Ming and Hou, Qibin},
  booktitle={European conference on computer vision},
  year={2024},
  organization={Springer}
}